Famille libre, famille liée
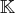 est le corps
est le corps
 ,
,
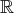 ou
ou
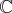 . On appelle scalaire tout élément de
. On appelle scalaire tout élément de
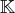 .
. Définition
Une famille de vecteurs
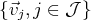 (où
(où
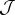 est un ensemble quelconque) d’un
est un ensemble quelconque) d’un
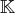 -espace
vectoriel
-espace
vectoriel
 est dite liée si il existe un entier
est dite liée si il existe un entier
 , des indices
, des indices
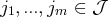 et des
scalaires
et des
scalaires
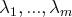 tels que :
tels que :
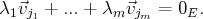
La famille
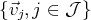 est dite libre si elle n’est pas liée.
est dite libre si elle n’est pas liée.
Ainsi, pour déterminer si une famille finie
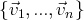 d’un
d’un
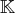 -espace vectoriel
-espace vectoriel
 est
libre ou liée, il suffit de déterminer l’ensemble des
est
libre ou liée, il suffit de déterminer l’ensemble des
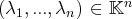 solutions
de :
solutions
de :

La famille
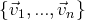 sera libre si la seule solution est
sera libre si la seule solution est
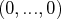 . Elle sera liée sinon.
. Elle sera liée sinon.

Toute famille infinie d’éléments de
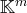 est nécessairement liée.
est nécessairement liée.
Soit
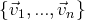 une famille finie de
une famille finie de
 . Voici deux méthodes permettant de
déterminer si cette famille est libre ou liée et permettant de plus, si elle est liée, de
déterminer les relations linéaires sur ses vecteurs :
. Voici deux méthodes permettant de
déterminer si cette famille est libre ou liée et permettant de plus, si elle est liée, de
déterminer les relations linéaires sur ses vecteurs :
 est de dimension finie
est de dimension finieDe même que dans le cas précédent, toute famille infinie d’éléments de
 est
nécessairement liée.
est
nécessairement liée.
Soit
 est un espace vectoriel de dimension finie
est un espace vectoriel de dimension finie
 sur
sur
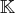 .
.
Soit
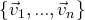 une famille finie de
une famille finie de
 .
.
Alors, on considère une base
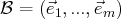 de
de
 . En utilisant l’écriture des vecteurs
dans la base
. En utilisant l’écriture des vecteurs
dans la base
 (voir l’élément de cours sur les bases) on se ramène au cas où
(voir l’élément de cours sur les bases) on se ramène au cas où
 de
la manière suivante :
de
la manière suivante :
Pour tout
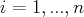 , il existe un unique
, il existe un unique
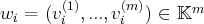 tel que
tel que
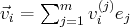 . De plus, si
. De plus, si
 sont des scalaires, l’égalité
sont des scalaires, l’égalité
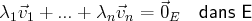
équivaut à l’égalité :
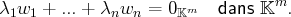
En particulier, la famille de vecteurs
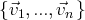 est libre dans
est libre dans
 si et seulement si la
famille
si et seulement si la
famille
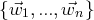 est libre dans
est libre dans
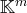 .
.
On se ramène ainsi au cas où
 .
.
Un exemple classique de
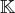 -espace vectoriel de dimension infinie est l’ensemble des
applications définies sur un même ensemble à valeurs dans
-espace vectoriel de dimension infinie est l’ensemble des
applications définies sur un même ensemble à valeurs dans
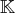 . L’espace vectoriel des suites
d’éléments de
. L’espace vectoriel des suites
d’éléments de
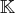 en est un cas particulier.
en est un cas particulier.
Soit
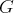 un ensemble quelqonque. Rappelons que l’ensemble
un ensemble quelqonque. Rappelons que l’ensemble
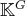 des applications de
des applications de
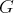 dans
dans
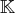 est muni de manière naturelle d’une structure de
est muni de manière naturelle d’une structure de
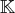 -espace vectoriel. Voir
l’élément de cours sur les espaces de fonctions.
-espace vectoriel. Voir
l’élément de cours sur les espaces de fonctions.
Soit une famille finie
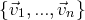 de
de
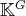 . Alors, les
. Alors, les
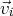 sont des applications de
sont des applications de
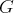 dans
dans
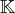 .
.
Soient des scalaires
 . Dire que
. Dire que
 signifie que :
signifie que :

De même pour les espaces de suites dans
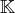 (on rappelle qu’une suite d’éléments de
(on rappelle qu’une suite d’éléments de
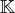 est une application de
est une application de
 dans
dans
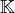 ).
).
Résolution d’un système d’équations linéaires
Déterminer l’ensemble des
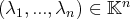 solutions de :
solutions de :

revient à résoudre le système d’équations linéaires à
 équations et d’inconnues
équations et d’inconnues
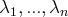 suivant :
suivant :
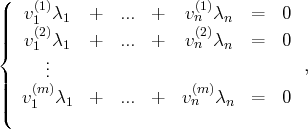
en notant, pour tout
 ,
,
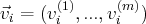 .
.
Voir le rappel de cours sur les systèmes déquations linéaires pour en savoir plus sur de
tels systèmes. La méthode de résolution de ces systèmes par le pivot de Gauss est
décrite dans l’élément de cours système d’équations linéaires ainsi qu’à la rubrique
méthode et techniques Échelonner un système linéaire par la méthode de Gauss .
Échelonnement de la famille de vecteurs
L’idée est d’utiliser la méthode du pivot de Gauss sur les vecteurs de manière à se ramener à une famille échelonnée de vecteurs. Ce paragraphe comporte quatre points :
Les opérations suivantes sur les familles de vecteurs n’ont pas d’incidence sur le caractère libre ou lié de la famille :
Ces opérations ont de plus la vertu de ne pas modifier le sous-espace vectoriel de
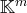 engendré
par la famille de vecteurs.
engendré
par la famille de vecteurs.
Familles échelonnées de vecteurs
Une famille de vecteurs
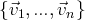 de
de
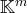 avec, pour tout
avec, pour tout
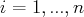 :
:
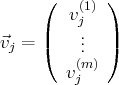
est dite échelonnée si il existe une suite strictement croissante d’entiers naturels
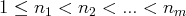 telle que :
telle que :
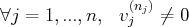
et
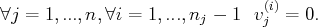
Par exemple, la famille de vecteurs suivante du
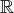 -espace vectoriel
-espace vectoriel
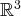 est échelonnée :
est échelonnée :
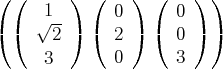
avec
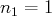 ,
,
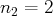 et
et
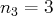 .
.
La famille de vecteurs suivante du
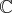 -espace vectoriel
-espace vectoriel
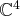 est échelonnée :
est échelonnée :
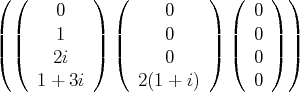
avec
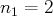 ,
,
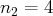 et
et
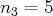 .
.
Il est facile de voir qu’une famille échelonnée de vecteurs de
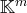 est libre si et seulement
si elle ne contient pas de vecteurs nuls. Ainsi la famille de
est libre si et seulement
si elle ne contient pas de vecteurs nuls. Ainsi la famille de
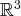 donnée en exemple est libre et
celle de
donnée en exemple est libre et
celle de
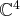 donnée en exemple est liée.
donnée en exemple est liée.
Échelonnement d’une famille de vecteurs par la méthode du pivot de Gauss :
théorie
La méthode que nous décrivons permet de se ramener à une famille échelonnée de
vecteurs en, au plus,
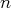 étapes (où
étapes (où
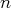 est le nombre de vecteurs de la famille
initiale). À l’issue de l’étape
est le nombre de vecteurs de la famille
initiale). À l’issue de l’étape
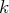 , la famille de vecteurs obtenue a la forme
, la famille de vecteurs obtenue a la forme
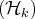 suivante :
suivante :
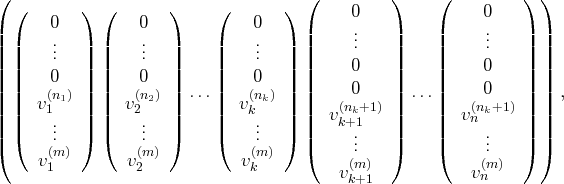
avec
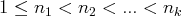 et
et
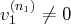 ,...,
,...,
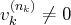 .
.
Décrivons l’étape
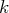 de la méthode :
de la méthode :
Étant donné une famille de la forme
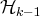 , nous allons la modifier de sorte à obtenir une
famille de la forme
, nous allons la modifier de sorte à obtenir une
famille de la forme
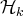 en n’utilisant que des opérations autorisées.
en n’utilisant que des opérations autorisées.
Nous noterons
 le
le
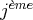 vecteur de la famille.
vecteur de la famille.
 premiers vecteurs de la famille.
premiers vecteurs de la famille.
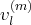 (avec
(avec
 et
et
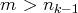 ) sont nuls, alors,
pour tout
) sont nuls, alors,
pour tout
 , le vecteur
, le vecteur
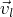 est nul. La famille a donc la forme voulue.
L’algorithme s’arrête.
est nul. La famille a donc la forme voulue.
L’algorithme s’arrête.
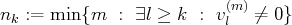 . Alors, quitte à échanger
le vecteur
. Alors, quitte à échanger
le vecteur
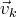 avec un vecteur
avec un vecteur
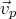 avec
avec
 (tel que
(tel que
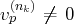 ), on se
ramène au cas où
), on se
ramène au cas où
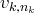 est non nul (ce sera notre pivot pour l’étape
est non nul (ce sera notre pivot pour l’étape
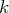 ).
).
 , on remplace
, on remplace
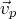 par
par
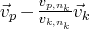 (afin d’éliminer les
(afin d’éliminer les
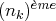 coordonnées
coordonnées
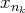 des vecteurs
des vecteurs
 .
.
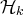 , l’étape
, l’étape
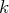 est
finie.
est
finie.
Illustration de la méthode sur deux exemples
Un exemple où la famille est libre
On considère les trois vecteurs suivants de
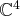 :
:
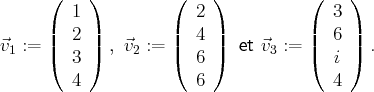
On souhaite savoir si la famille
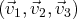 de
de
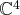 est libre ou liée et, si elle est liée,
déterminer les relations linéaires existant entre les trois vecteurs.
est libre ou liée et, si elle est liée,
déterminer les relations linéaires existant entre les trois vecteurs.
Les familles de vecteurs suivantes sont libres ou liées simultanément :
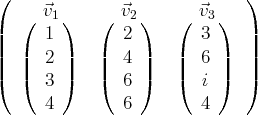
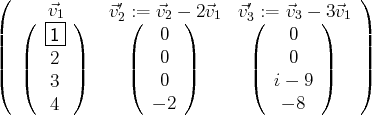
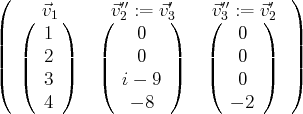
Cette dernière famille de vecteurs de
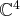 est échelonnée et libre (car elle ne contient pas de
vecteur nul). Ainsi
est échelonnée et libre (car elle ne contient pas de
vecteur nul). Ainsi
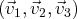 est une famille libre de
est une famille libre de
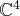 .
.
Un exemple où la famille est liée par deux relations linéaires indépendantes
On considère les quatre vecteurs suivants de
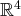 :
:

On souhaite savoir si la famille
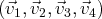 de
de
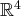 est libre ou liée et, si elle est liée,
d
est libre ou liée et, si elle est liée,
d
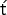 erminer les relations linéaires existant entre les quatre vecteurs.
erminer les relations linéaires existant entre les quatre vecteurs.
Les familles de vecteurs suivantes sont libres ou liées simultanément :
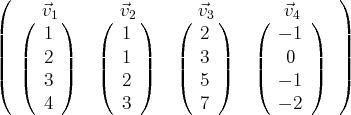
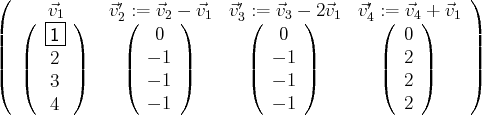
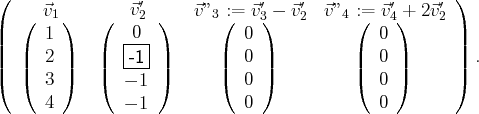
Cette dernière famille de vecteurs de
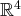 est échelonnée et liée (car elle contient
des vecteurs nuls). Ainsi
est échelonnée et liée (car elle contient
des vecteurs nuls). Ainsi
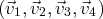 est une famille liée de
est une famille liée de
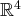 . De plus, on
a :
. De plus, on
a :
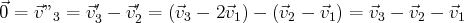
et
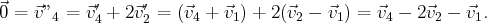
Ainsi, on a les relations linéaires suivantes :

et
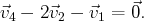
De plus, les relations linéaires liant
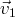 ,
,
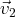 ,
,
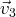 et
et
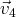 sont les relations s’écrivant comme
une combinaison lináire de ces deux relations, c’est-à-dire que ce sont les relations de la
forme :
sont les relations s’écrivant comme
une combinaison lináire de ces deux relations, c’est-à-dire que ce sont les relations de la
forme :
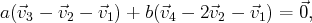
avec
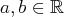 . Autrement dit, les relations linéaires liant
. Autrement dit, les relations linéaires liant
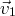 ,
,
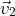 ,
,
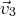 et
et
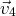 sont les
relations de la forme :
sont les
relations de la forme :
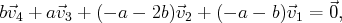
avec
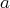 et
et
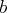 deux réels quelconques.
deux réels quelconques.
Remarque : si on souhaite simplement prouver que le système de vecteurs
est lié, il n’est pas nécessaire de déterminer ,toutes les relations linéaires existant
entre les vecteurs du système : il suffit de trouver une relation linéaire non nulle ;
par exemple, ici, il suffisait de remarquer que
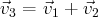 ce qui nous donne
directement :
ce qui nous donne
directement :
 et nous assure que le système
et nous assure que le système
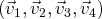 est lié.
est lié.