Méthode de Gauss pour les systèmes d’équations linéaires
On cherche, en utilisant ces opérations, à obtenir un système échelonné que l’on saura résoudre
aisément. Pour expliquer ce que veut dire échelonner un système et comment le résoudre, le
plus simple est de commencer par un exemple.
Considérons le système dont les inconnues sont
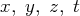 et où
et où
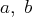 sont des paramètres
fixés.
sont des paramètres
fixés.
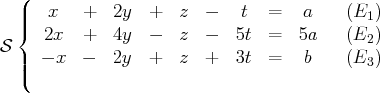
Choisissons une équation avec un coefficient non nul pour la première inconnue
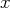 .
Ici la première équation convient avec le coefficient 1, pour
.
Ici la première équation convient avec le coefficient 1, pour
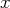 , qu’on appelle le
premier pivot. On va utiliser ce pivot de notre algorithme pour faire disparaître
l’inconnue
, qu’on appelle le
premier pivot. On va utiliser ce pivot de notre algorithme pour faire disparaître
l’inconnue
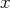 des autres équations. On obtient un système linéaire équivalent :
des autres équations. On obtient un système linéaire équivalent :
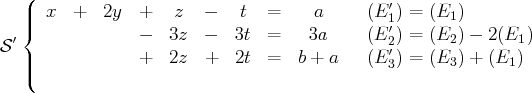
Laissons de côté la première équation que l’on utilisera à la fin pour calculer
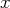 . On
remarque que dans les deux dernières équations la variable suivante
. On
remarque que dans les deux dernières équations la variable suivante
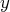 n’apparaît pas. On
est ramené à un système de deux équations avec ici deux variables en moins. Choisissons
notre deuxième pivot. On le trouve dans l’équation
n’apparaît pas. On
est ramené à un système de deux équations avec ici deux variables en moins. Choisissons
notre deuxième pivot. On le trouve dans l’équation
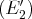 . C’est le coefficient
. C’est le coefficient
 de
de
 .
Nous allons l’utiliser pour éliminer
.
Nous allons l’utiliser pour éliminer
 des équations suivantes (ici, il n’en reste qu’une).
Réécrivons notre nouveau système :
des équations suivantes (ici, il n’en reste qu’une).
Réécrivons notre nouveau système :
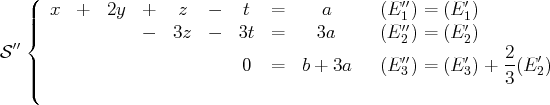
Remarques
 . On remarque que dans la
troisième équation la variable suivante
. On remarque que dans la
troisième équation la variable suivante
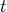 n’apparaît pas.
n’apparaît pas.Le système
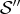 a des solutions si et seulement si les paramètres
a des solutions si et seulement si les paramètres
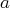 et
et
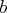 vérifient
vérifient
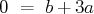
 .
.
Quand ce système a des solutions (si
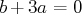 ), on détermine les solutions en remontant.
Chaque marche permet de calculer une des lettres (on choisit celle qui est au coin de la
marche) en fonction des lettres suivantes.
), on détermine les solutions en remontant.
Chaque marche permet de calculer une des lettres (on choisit celle qui est au coin de la
marche) en fonction des lettres suivantes.
Ainsi, on peut trouver
 puis
puis
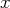 en fonction des variables libres (celles qui se trouvent sur
le plat des marches)
en fonction des variables libres (celles qui se trouvent sur
le plat des marches)
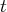 et
et
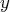 . On obtient
. On obtient

Puis,
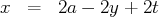
L’ensemble des solutions peut s’écrire :
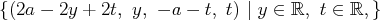
Remarque : On peut écrire les composantes des solutions dans la base canonique de
 sous la forme :
sous la forme :
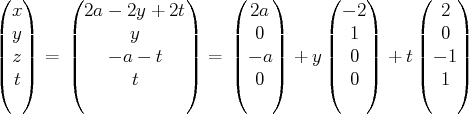
L’ensemble des solutions peut donc s’écrire
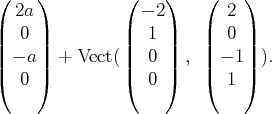
Les solutions forment un espace affine de dimension
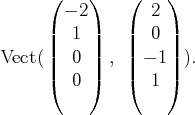
 . C’est le translaté du sous espace
vectoriel :
. C’est le translaté du sous espace
vectoriel :
Avec cet exemple on peut comprendre facilement le fonctionnement de l’algorithme pour un système quelconque d’équations.
 dans
une des équations. Par permutation, cette équation devient la première équation.
dans
une des équations. Par permutation, cette équation devient la première équation.
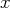 des équations suivantes.
des équations suivantes.
 on les place en
dernier.
on les place en
dernier.
L’algorithme s’arrête lorsqu’il ne reste plus que des équations
 . Les premières équations
sont échelonnées.
. Les premières équations
sont échelonnées.
Le système admet des solutions si et seulement si les équations
 sont vérifiées et
dans ce cas on obtient les solutions en calculant les inconnues “coin de marche”,
dites inconnues principales en fonction des autres inconnues, dites variables libres.
sont vérifiées et
dans ce cas on obtient les solutions en calculant les inconnues “coin de marche”,
dites inconnues principales en fonction des autres inconnues, dites variables libres.
Voici un autre exemple déjà échelonné dans
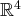 pour bien comprendre ces notions
d’inconnues principales et de variables libres. La lettre
pour bien comprendre ces notions
d’inconnues principales et de variables libres. La lettre
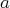 désigne un paramètre réel fixé. Les
inconnues
désigne un paramètre réel fixé. Les
inconnues
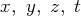 vérifient les deux équations :
vérifient les deux équations :
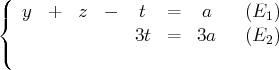
On choisit comme inconnues principales
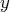 et
et
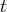 et comme variables libres
et comme variables libres
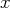 et
et
 .
L’ensemble des solutions est
.
L’ensemble des solutions est
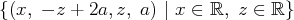
Ce choix n’est pas unique. Par exemple, en permutant l’ordre des variables on obtient un autre escalier
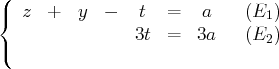
Cet escalier conduit à un autre choix pour les inconnues principales
 et
et
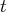 et pour les
variables libres
et pour les
variables libres
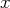 et
et
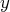 .
.