Algèbre linéaire
Elément de cours des exercices
Les espaces de fonctions réelles
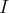un intervalle de
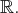On note
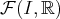l’ensemble des applications de
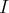dans
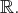
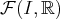est un espace vectoriel sur
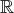; c’est un espace de dimension infinie.
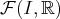est l’application nulle, c’est-à-dire l’application qui, à tout
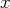de
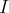, associe le réel zéro. 
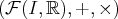en sont des sous-espaces
vectoriels ;
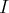dans
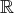continues, noté
;
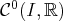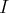dans
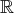de classe
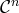, noté
;
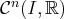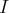dans
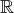de classe
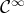, noté
;
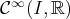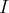est symétrique par rapport à 0, l’ensemble des applications paires
(respectivement impaires) de
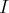dans
.
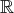