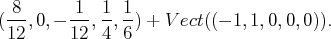Système d’équations linéaires
Ici, nous considérons que
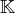 est le corps
est le corps
 ,
,
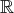 ou
ou
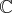 .
.
Un système d’équations linéaires à
 équations et
équations et
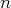 inconnues s’écrit :
inconnues s’écrit :
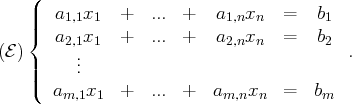
Dans ce système linéaire, les coefficients
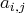 sont connus ; de même que les scalaires
sont connus ; de même que les scalaires
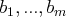 . Les inconnues sont les
. Les inconnues sont les
 .
.
Résoudre ce système signifie déterminer l’ensemble des
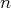 -uplets
-uplets
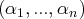 de
de
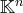 qui en sont solutions, c’est à dire tel que :
qui en sont solutions, c’est à dire tel que :

Un conseil à suivre : lorsque vous écrivez un système d’équations linéaires,
efforcez vous de faire apparaître les inconnues
 en dessous des inconnues
en dessous des inconnues
 :
:
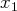 de la seconde équation en dessous de
de la seconde équation en dessous de
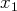 de la première équation, de même pour
de la première équation, de même pour
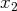 et ainsi de suite.
et ainsi de suite.
Nous détaillons ici la méthode du pivot de Gauss pour la résolution de systèmes d’équations linéaires. L’idée consiste à se ramener à un système équivalent plus simple à résoudre (échelonné). Notre plan est le suivant :
Signalons que si on connaît une solution particulière
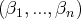 de ce système, alors
de ce système, alors
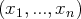 est solution de ce système si et seulement si
est solution de ce système si et seulement si
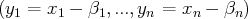 est solution du système linéaire ”homogène” associé :
est solution du système linéaire ”homogène” associé :

Nous n’utilisons pas ce point de vue ici mais nous renvoyons à ICI pour plus de détails.
Remarquons seulement que le système
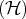 admet toujours au moins une solution :
admet toujours au moins une solution :
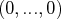 .
.
Remarquons, d’autre part, que si
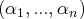 et
et
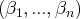 sont deux solutions de notre
système
sont deux solutions de notre
système
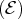 , alors tous les
, alors tous les
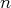 -uplets de la forme
-uplets de la forme
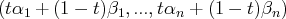 avec
avec
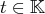 sont encore solutions de
sont encore solutions de
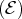 .
.
Questions amenant à des résolutions de systèmes d’équations linéaires
D’un point de vue matriciel, le système
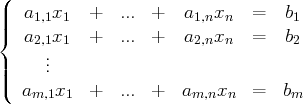
s’écrit
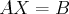 où
où
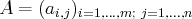 est une matrice à
est une matrice à
 lignes et
lignes et
 colonnes,
où
colonnes,
où
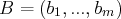 est un vecteur de
est un vecteur de
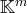 et où
et où
 est un vecteur de
est un vecteur de
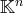 inconnu.
inconnu.
Questions amenant à des résolutions de systèmes d’équations linéaires
En algèbre linéaire, on est souvent amené à la résolution de systèmes d’équations
linéaires. Ici
 et
et
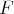 désignent des
désignent des
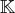 -espaces vectoriels quelconques de dimension finie.
Voici quelques exemples de problèmes être traités en résolvant un système d’équations
linéaires :
-espaces vectoriels quelconques de dimension finie.
Voici quelques exemples de problèmes être traités en résolvant un système d’équations
linéaires :
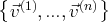 est libre, revient à
déterminer l’ensemble des
est libre, revient à
déterminer l’ensemble des
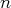 -uplets
-uplets
 tels que
tels que
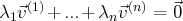 .
.
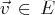 comme combinaison linéaire de vecteurs
comme combinaison linéaire de vecteurs
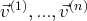 (de
(de
 ) revient à déterminer l’ensemble des
) revient à déterminer l’ensemble des
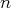 -uplets
-uplets
 tels que
tels que
 .
.
 et si
et si
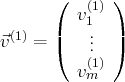 ,
,
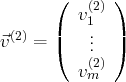 ,...,
,...,
 et
et
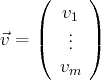 , alors l’égalité
, alors l’égalité
 s’écrit :
s’écrit :
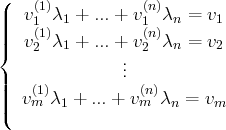
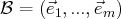 de
de
 . Pour tout
. Pour tout
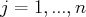 , nous
notons
, nous
notons
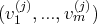 les coordonnées de
les coordonnées de
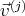 dans la base
dans la base
 et on écrit l’égalité
et on écrit l’égalité
 exprimée dans la base
exprimée dans la base
 . Nous nous ramenons ainsi à un
système d’équations linéaires de la même forme que dans le cas où
. Nous nous ramenons ainsi à un
système d’équations linéaires de la même forme que dans le cas où
 .
.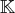 -linéaire
-linéaire
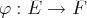 se ramène à résoudre
se ramène à résoudre
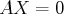 où
où
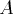 est la matrice associée à
est la matrice associée à
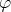 dans une base (quelconque). Le noyau
de
dans une base (quelconque). Le noyau
de
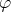 est l’ensemble des antécédents de
est l’ensemble des antécédents de
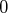 par
par
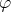 . Voir ! ! ! ! ! ! (lien vers ”écriture
matricielle”)
. Voir ! ! ! ! ! ! (lien vers ӎcriture
matricielle”)
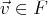 par une application linéaire
par une application linéaire
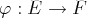 revient à résoudre
revient à résoudre
 , en utilisant l’écriture matricielle.
, en utilisant l’écriture matricielle.
Systèmes équivalents, opérations autorisées
Deux systèmes d’équations linéaires sont dits équivalents si ils ont les mêmes inconnues et les mêmes solutions.
Les opérations suivantes transforment un système d’équations linéaires en un système d’équations linéaires équivalent :
Par exemple (ici
 ), les systèmes suivants sont équivalents :
), les systèmes suivants sont équivalents :
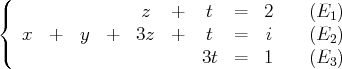
(échangeons les deux premières équations)
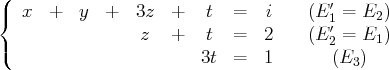
(Divisons la troisième équation par 3 de sorte à déterminer la valeur de
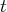 )
)
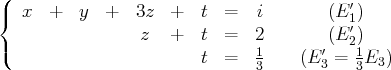
(Éliminons
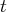 des autres équations)
des autres équations)
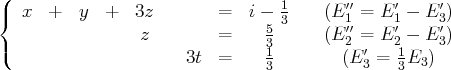
(Éliminons
 de la première équation)
de la première équation)
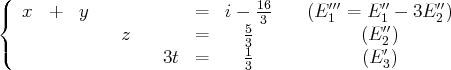
Ainsi, l’ensemble des solutions de

est l’ensemble des quadruplets
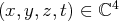 tels que :
tels que :
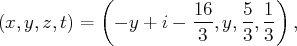
c’est-à-dire tels que :
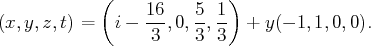
L’ensemble des solution est donc :
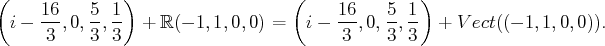
Des systèmes faciles à résoudre : les systèmes échelonnés
Un système d’équations linéaires :
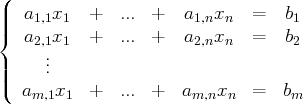
est dit échelonné s’il existe une suite (finie) strictement croissante d’entiers
 telle que :
telle que :
 et tout
et tout
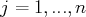 tel que
tel que
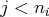 , on a :
, on a :
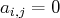 ;
;
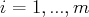 , on a :
, on a :
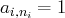 .
.C’est-à-dire que le système est de la forme :
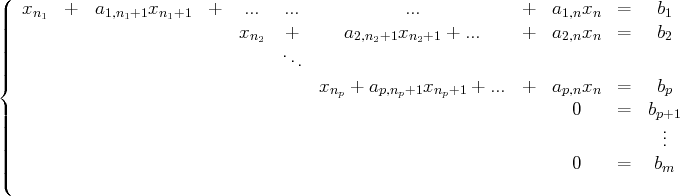
avec
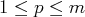 et
et
 .
.
Voici trois exemples de systèmes échelonnés :
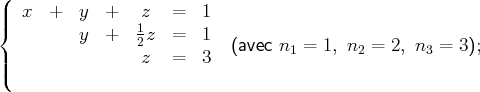
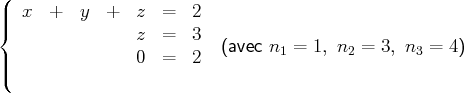
et
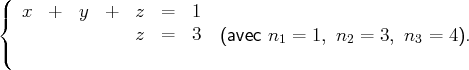
Résolution de systèmes échelonnés : théorie
Un tel système est facile à résoudre :
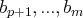 est nul, alors le système n’admet pas de solution.
est nul, alors le système n’admet pas de solution.
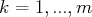 , notons
, notons
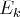 la
la
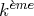 équation du système. Voici une méthode pour résoudre ce système :
équation du système. Voici une méthode pour résoudre ce système :
On commence par éliminer les termes en
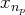 des
des
 premières équations
(en remplaçant l’équation
premières équations
(en remplaçant l’équation
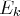 par
par
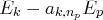 pour tout
pour tout
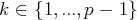 ).
).
Puis on recommence avec
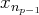 : on élimine les termes en
: on élimine les termes en
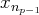 des
des
 premières équations (en remplaçant
premières équations (en remplaçant
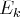 par
par
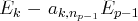 pour tout
pour tout
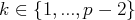 ). Et ainsi de suite.
). Et ainsi de suite.
En procédant de la sorte, on obtient finalement un système exprimant les
inconnues
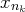 (pour
(pour
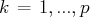 ) en fonction des autres inconnues, ce qui
nous permet de résoudre le système.
) en fonction des autres inconnues, ce qui
nous permet de résoudre le système.
Résolution de systèmes échelonnés : pratique
Nous allons à présent résoudre les trois systèmes donnés précédemment en exemple.
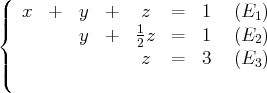
 des deux premières équations)
des deux premières équations)
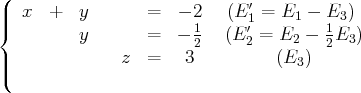
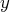 de la première équation)
de la première équation)
Ainsi, le premier système admet pour unique solution
 . C’est-à-dire
que l’ensemble de ses solutions est :
. C’est-à-dire
que l’ensemble de ses solutions est :
 .
.
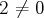 , le deuxième système n’admet pas de solution. C’est-à-dire que
l’ensemble de ses solutions est
, le deuxième système n’admet pas de solution. C’est-à-dire que
l’ensemble de ses solutions est
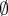 .
.
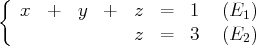
(éliminons
 de la première équation)
de la première équation)
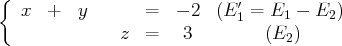
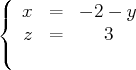
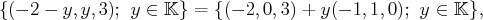
c’est-à-dire :
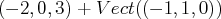 .
.
Résolution par la méthode du pivot de Gauss (théorie)
La méthode du pivot de Gauss pour les systèmes d’équations linéaires transforme un
système d’équations linéaires en un système d’équations linéaires échelonné équivalent. Cette
méthode utilise uniquement les deux types d’opérations autorisées vues précédemment. Cette
méthode se fait en, au plus,
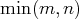 étapes telles qu’à l’issue de l’étape
étapes telles qu’à l’issue de l’étape
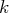 , le système
obtenu ait la forme
, le système
obtenu ait la forme
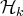 suivante :
suivante :

avec
 .
.
Nous décrivons à présent l’étape
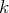 de la méthode du Pivot de Gauss : Étant donné un
système de la forme
de la méthode du Pivot de Gauss : Étant donné un
système de la forme
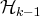 , nous allons le transformer de sorte à obtenir un système de la
forme
, nous allons le transformer de sorte à obtenir un système de la
forme
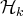 .
.
Nous noterons
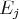 la
la
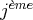 équation du système.
équation du système.
 premières équations du système linéaire.
premières équations du système linéaire.
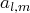 (avec
(avec
 et
et
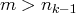 ) sont nuls, alors, pour
tout
) sont nuls, alors, pour
tout
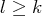 , l’équation
, l’équation
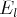 s’écrit :
s’écrit :
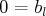 . Le système a donc la forme voulue.
L’algorithme s’arrête.
. Le système a donc la forme voulue.
L’algorithme s’arrête.
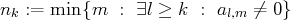 . Alors, quitte à échanger
la ligne
. Alors, quitte à échanger
la ligne
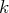 avec une ligne
avec une ligne
 (telle que
(telle que
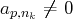 ), on se ramène au cas
où
), on se ramène au cas
où
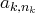 est non nul (ce sera notre pivot pour l’étape
est non nul (ce sera notre pivot pour l’étape
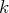 ).
).
On remplace alors l’équation
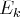 par
par
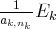 pour se ramener à :
pour se ramener à :
 .
.
 , on remplace
, on remplace
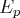 par
par
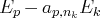 (afin d’éliminer les
termes en
(afin d’éliminer les
termes en
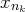 des équations
des équations
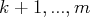 ).
).
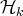 , l’étape
, l’étape
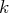 est finie.
est finie.
Illustration de la méthode du pivot de Gauss sur des exemples
On veut résoudre le système suivant dans
 :
:
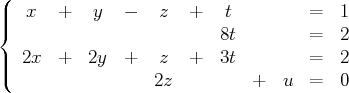
Nous utilisons la méthode du Pivot de Gauss (à chaque étape, le pivot est encadré). Les systèmes d’équations linéaires suivants sont équivalents :
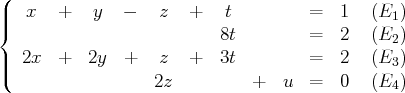
(il y a un terme en
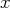 dans la première équation, notre premier pivot de Gauss sera ce
terme : nous l’utilisons pour éliminer les termes en
dans la première équation, notre premier pivot de Gauss sera ce
terme : nous l’utilisons pour éliminer les termes en
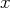 des autres équations)
des autres équations)
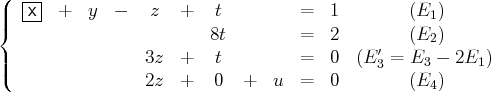
(nous oublions à présent la première ligne ; il n’y a pas de terme en
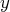 dans les équations
dans les équations
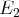 ,
,
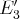 et
et
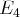 ; il y a un terme en
; il y a un terme en
 dans
dans
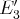 mais pas dans
mais pas dans
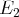 ; nous permutons donc les
équations
; nous permutons donc les
équations
 et
et
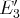 )
)
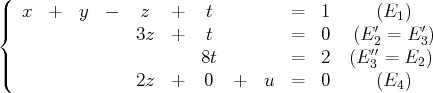
(nous divisons la deuxième équation par 3 de sorte à avoir
 au lieu de
au lieu de
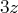 dans la
deuxième équation)
dans la
deuxième équation)
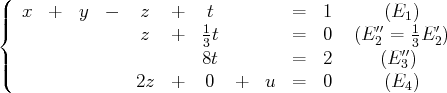
(le terme en
 de la deuxième équation est notre nouveau pivot de Gauss ; nous l’utilisons
pour éliminer les termes en
de la deuxième équation est notre nouveau pivot de Gauss ; nous l’utilisons
pour éliminer les termes en
 des équations situés en dessous)
des équations situés en dessous)
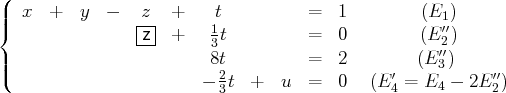
(nous oublions à présent la deuxième équation ; il y a un terme en
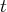 dans la troisième
équation, nous divisons la troisième équation par 8 de sorte à avoir
dans la troisième
équation, nous divisons la troisième équation par 8 de sorte à avoir
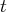 à la place de
à la place de
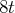 dans
cette équation)
dans
cette équation)
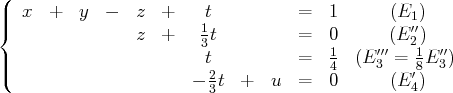
(le terme en
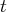 de la troisième équation devient notre nouveau pivot de Gauss : nous
l’utilisons pour éliminer les termes en
de la troisième équation devient notre nouveau pivot de Gauss : nous
l’utilisons pour éliminer les termes en
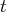 de la quatrième équation)
de la quatrième équation)
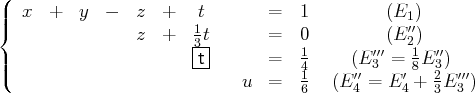
Ce système d’équations linéaires est échelonné et équivalent à notre système initial.
Nous le résolvons en appliquant la méthode expliquée ICI pour la théorie et ICI pour la pratique sur des exemples. Notre système est équivalent aux systèmes suivants :
(utilisons la dernière équation pour éliminer
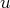 des autres équations : inutile il n’y a pas
de
des autres équations : inutile il n’y a pas
de
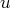 dans les autres équations ; utilisons la troisième équation pour éliminer les termes en
dans les autres équations ; utilisons la troisième équation pour éliminer les termes en
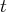 des deux premières équations)
des deux premières équations)

(utilisons la deuxième équation pour éliminer
 de la première)
de la première)
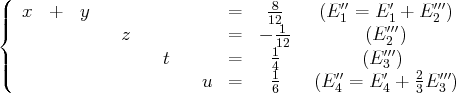
(Le dernier système obtenu donne une expression de
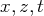 en fonction de
en fonction de
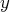 ).
Ainsi, notre système admet une infinité de solutions et l’ensemble de ses solutions
est :
).
Ainsi, notre système admet une infinité de solutions et l’ensemble de ses solutions
est :
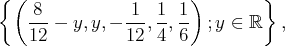
c’est-à-dire :
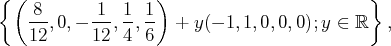
ce qui s’écrit encore :