Algèbre linéaire
Elément de cours des exercices
Base dans un espace vectoriel de dimension finie.
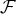est-elle une base de
espace vectoriel de
dimension finie ? ”
Définition : Soit
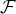une famille de vecteurs d’un espace vectoriel
. Dire que
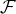est une base de
signifie que
est une famille libre et génératrice de
.
Définition : Soit
un
-espace vectoriel.
est de dimension finie signifie que
admet une famille génératrice finie.
Théorème : Toutes les bases d’un espace vectoriel de dimension finie ont même cardinal
.
est appelé la dimension de
.
Théorème : Soit
un espace vectoriel de dimension
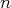et soit
une famille finie de
vecteurs de
. Les propositions sont équivalentes :
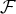est une base de
.
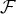est une famille libre et génératrice de
.
est une famille libre de
et le cardinal de
est égal à
.
est une famille génératrice de
et le cardinal de
est égal à
. Pour répondre à la question : ”
est-elle une base de
espace vectoriel de
dimension finie ? ” :
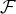n’est pas une famille libre par exemple si l’on ”voit ” une relation linéaire
liant les vecteurs de
on peut tout de suite dire que
n’est pas une base
de
.
,
n’est pas égal à la dimension de l’espace
on peut
tout de suite dire que
n’est pas une base de
.
est égal à la dimension de l’espace
, le plus souvent
on vérifie simplement que la famille
est une famille libre pour conclure
qu’elle forme une base de
.
est égal à la dimension de l’espace
, il arrive parfois
que l’on montre que la famille
est génératrice .
Par exemple soit :
une famille de polynômes de
![ℝn [X ]](cst50x.png)
tel que pour tous
,
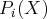est unitaire et de degré
.
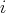On montre par récurrence pour tous
que :
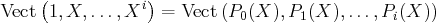
On a donc
![Vect (P (X ),P (X ),...,P (X )) = Vect (1,X, ...,Xn ) = ℝ [X ]
0 1 n n](cst56x.png)
Donc
est une famille génératrice de
![ℝn [X ]](cst58x.png)
de cardinal
. Or la
dimension de
![ℝ [X ]
n](cst60x.png)
est égale à
. Donc
est une base de
![ℝ [X ]
n](cst63x.png)
.