Familles génératrices.
1. Définition.
1. Définition. Soit
 un
un
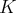 -espace vectoriel et
-espace vectoriel et
 une famille de vecteurs de
une famille de vecteurs de
 .
.
La famille
 est une famille génératrice de
est une famille génératrice de
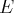 si tout vecteur de
si tout vecteur de
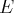 est une combinaison linéaire des vecteurs
est une combinaison linéaire des vecteurs
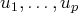 , c’est-à-dire si pour tout
vecteur
, c’est-à-dire si pour tout
vecteur
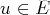 , il existe
, il existe
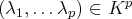 tel que
tel que
 .
.
Exemple. Soit
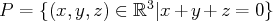 . On a
. On a
 , donc
, donc
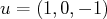 et
et
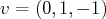 sont des vecteurs de
sont des vecteurs de
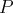 et tout vecteur de
et tout vecteur de
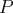 est
une combinaison linéaire de ces deux vecteurs. La famille
est
une combinaison linéaire de ces deux vecteurs. La famille
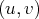 est une famille génératrice
de
est une famille génératrice
de
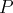 .
.
Généralisation. Une famille
 de vecteurs de
de vecteurs de
 indexée par un ensemble
indexée par un ensemble
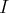 infini
est une famille génératrice de
infini
est une famille génératrice de
 si tout vecteur de
si tout vecteur de
 est combinaison linéaire d’une
sous-famille finie de
est combinaison linéaire d’une
sous-famille finie de
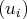 . Par exemple, la famille des monômes
. Par exemple, la famille des monômes
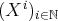 est une famille
génératrice de
est une famille
génératrice de
![ℝ [X ]](cst26x.png) .
.
1. Familles génératrices et bases.
Définition. Une base de
 est une famille de
est une famille de
 qui est génératrice et libre.
qui est génératrice et libre.
Exemple. La famille
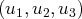 des trois vecteurs de
des trois vecteurs de
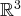 donnés par
donnés par
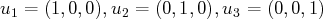 est une famille génératrice de
est une famille génératrice de
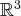 . C’est même
une base, dite base canonique de
. C’est même
une base, dite base canonique de
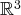 .
.
3. Familles génératrices et applications linéaires.
Proposition. Soit
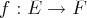 une application linéaire et
une application linéaire et
 une famille
génératrice de
une famille
génératrice de
 .
.
La famille
 est une famille génératrice de l’image
est une famille génératrice de l’image
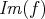 .
.
Remarques.
 est une base de
est une base de
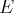 .
(Attention, la famille
.
(Attention, la famille
 n’est pas forcément pour autant une
base de
n’est pas forcément pour autant une
base de
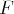 .)
.)
 qui n’est pas de dimension finie,
comme par exemple
qui n’est pas de dimension finie,
comme par exemple
![ℝ [X ]](cst44x.png) .
. 4. Familles génératrices en dimension finie.
En dimension finie, le théorème de la base incomplète donne les résultats suivants, qui
permettent souvent de décider si une famille est génératrice, plus facilement qu’à partir de la
définition :
Théorème 1. Soit
 un espace vectoriel de dimension finie de dimension finie, dim
un espace vectoriel de dimension finie de dimension finie, dim
 .
.
Si
 est une famille génératrice de
est une famille génératrice de
 , on a
, on a
 .
.
Théorème 2. Soit
 un espace vectoriel de dimension finie, dim
un espace vectoriel de dimension finie, dim
 .
.
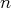 vecteurs qui engendre
vecteurs qui engendre
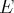 est une base de
est une base de
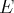 .
.
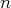 vecteurs de
vecteurs de
 est une base de
est une base de
 .
. Corollaire. Soit
 un espace vectoriel de dimension finie, dim
un espace vectoriel de dimension finie, dim
 et
et
 une famille de vecteurs de
une famille de vecteurs de
 .
.
Les trois énoncés suivants sont équivalents :
 est une famille génératrice de
est une famille génératrice de
 et
et
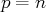 ;
;
 est une base de
est une base de
 ;
;
 est une famille libre et
est une famille libre et
 .
.