Algèbre linéaire
Elément de cours des exercices
Les espaces de matrices
 le corps
le corps
 ou
ou
 . Une matrice à
. Une matrice à
 lignes et
lignes et
 colonnes à coefficients dans
colonnes à coefficients dans
 est
une famille
est
une famille
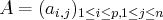 d’éléments de
d’éléments de
 L’ensemble de ces matrices est noté
L’ensemble de ces matrices est noté
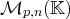 . Si
. Si
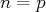 , on le note
, on le note
 .
.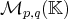 une loi appelée addition des matrices par : si
une loi appelée addition des matrices par : si
 et
et
 , alors
, alors

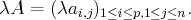

 est la matrice
est la matrice

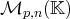 est de dimension
est de dimension
 Une base est constituée par les
Une base est constituée par les
 matrices
matrices
 avec
avec
 et
et
 définies comme ayant tous leurs termes nuls sauf celui situé
à la
définies comme ayant tous leurs termes nuls sauf celui situé
à la
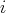 -ème ligne et
-ème ligne et
 -ème colonne qui vaut 1.
-ème colonne qui vaut 1.  est
est
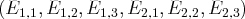 avec
avec
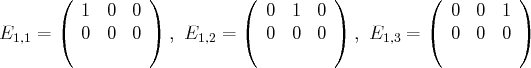

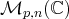 est également un espace vectoriel sur
est également un espace vectoriel sur
 ; dans ce cas, il est de
dimension
; dans ce cas, il est de
dimension
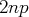 . Une base est donnée par les
. Une base est donnée par les
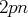 matrices
matrices
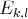 pour
pour
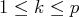 et
et
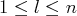 et
et
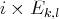 pour
pour
 et
et
 .
. en sont des sous-espaces vectoriels ;
en sont des sous-espaces vectoriels ;
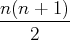 ;
;
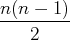 ;
;
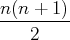 .
.