Algèbre linéaire
Elément de cours des exercices
 et
et
 : des espaces de
: des espaces de
 uplets
uplets
On note
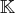 l’ensemble des réels ou des complexes. Si
l’ensemble des réels ou des complexes. Si
 est un entier, on désigne
par
est un entier, on désigne
par
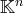 le produit cartésien
le produit cartésien
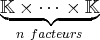 .
.
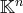 est donc l’ensemble des
est donc l’ensemble des
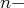 uplets ordonnés
uplets ordonnés
 d’éléments de
d’éléments de
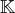 .
.
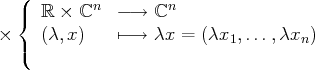
On définit, sur
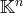 , deux lois appelées addition et multiplication par un scalaire :
, deux lois appelées addition et multiplication par un scalaire :
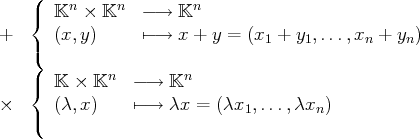
 sur
sur
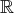 et
et
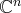 sur
sur
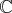 .
.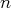 et ont pour base canonique les
et ont pour base canonique les
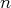 vecteurs
vecteurs
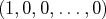 ,
,
 Le vecteur nul est
Le vecteur nul est
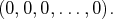
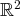 est un espace vectoriel sur
est un espace vectoriel sur
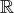 de dimension 2 dont une base est
de dimension 2 dont une base est
 .
. 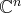 une loi appelée multiplication par un réel :
une loi appelée multiplication par un réel :
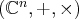 est alors un espace vectoriel sur
est alors un espace vectoriel sur
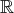 ; il est de dimension
; il est de dimension
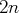 et
la base canonique de
et
la base canonique de
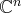 en tant que
en tant que
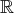 -espace vectoriel est formée des
-espace vectoriel est formée des
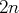 vecteurs
vecteurs
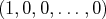 ,
,

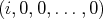 ,
,

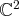 est un espace vectoriel
est un espace vectoriel
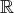 de dimension 4 dont une base est
de dimension 4 dont une base est