Algèbre linéaire
Elément de cours des exercices
Les espaces de fonctions
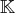 le corps des réels ou celui des complexes et
le corps des réels ou celui des complexes et
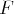 un espace vectoriel sur
un espace vectoriel sur
 Si
Si
 est un ensemble, on note
est un ensemble, on note
 l’ensemble des applications de
l’ensemble des applications de
 dans
dans
 .
.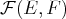 , une loi appelée addition des applications
, une loi appelée addition des applications

 est l’application définie par
est l’application définie par
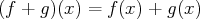 pour tout
pour tout
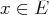 ,
,

 est l’application définie par
est l’application définie par
 pour tout
pour tout
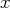 dans
dans
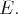
 est un espace vectoriel sur
est un espace vectoriel sur
 Il est de
dimension infinie.
Il est de
dimension infinie. est l’application nulle définie comme étant l’application qui, à
tout
est l’application nulle définie comme étant l’application qui, à
tout
 de
de
 , associe le vecteur nul de l’espace vectoriel
, associe le vecteur nul de l’espace vectoriel

 est un espace vectoriel sur
est un espace vectoriel sur
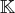 , l’ensemble des applications linéaires de
, l’ensemble des applications linéaires de
 dans
dans
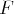 , noté
, noté
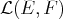 . Si
. Si
 , on le note
, on le note
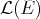 . Si
. Si
 et
et
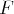 sont
de dimension finie, alors
sont
de dimension finie, alors
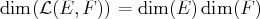 ;
;
 est un espace vectoriel sur
est un espace vectoriel sur
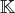 , l’ensemble des automorphismes de
, l’ensemble des automorphismes de
 noté
noté
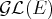 et appelé groupe linéaire de
et appelé groupe linéaire de
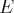 . C’est aussi un sous-espace vectoriel
de
. C’est aussi un sous-espace vectoriel
de
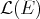 .
.