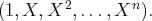Algèbre linéaire
Elément de cours des exercices
Les espaces de polynômes
![ℝ[X ]](cst0x.png) l’ensemble des polynômes à coefficients réels et
l’ensemble des polynômes à coefficients réels et
![ℂ[X ]](cst1x.png) l’ensemble des
polynômes à coefficents complexes. Muni de l’addition des fonctions et de la multiplication
d’une fonction par un réel, ces deux ensembles sont des espaces vectoriels sur
l’ensemble des
polynômes à coefficents complexes. Muni de l’addition des fonctions et de la multiplication
d’une fonction par un réel, ces deux ensembles sont des espaces vectoriels sur
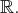 Ils sont de
dimension infinie.
Ils sont de
dimension infinie. ![ℂ[X ]](cst3x.png) est un espace vectoriel sur
est un espace vectoriel sur
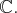 Il est de dimension infinie.
Il est de dimension infinie.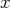 ,
associe le réel zéro.
,
associe le réel zéro.![ℝ [X ]](cst6x.png) et
et
![ℂ[X ]](cst7x.png) en sont des sous-espaces
vectoriels ;
en sont des sous-espaces
vectoriels ;
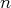 ,
noté
,
noté
![ℝ [X ]
n](cst9x.png) ; c’est un espace sur
; c’est un espace sur
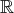 de dimension
de dimension
 Sa base canonique
est
Sa base canonique
est
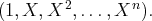
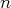 ,
noté
,
noté
![ℂn [X ]](cst14x.png) ; c’est un espace sur
; c’est un espace sur
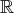 de dimension
de dimension
 Sa base canonique est
Sa base canonique est
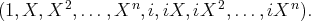 C’est également un espace vectoriel
sur
C’est également un espace vectoriel
sur
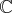 ; il est alors de dimension
; il est alors de dimension
 Sa base canonique, en tant que
Sa base canonique, en tant que
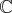 -espace vectoriel, est
-espace vectoriel, est