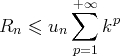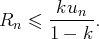Majoration des restes de séries
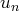 est convergente, on note
est convergente, on note
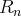 son reste d’ordre
son reste d’ordre
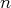 :
:
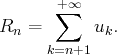
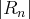 dans le cas des séries alternées
dans le cas des séries alternées
Théorème. Une série alternée, dont la valeur absolue du terme général
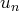 décroît
et tend vers 0, converge et on a, pour tout
décroît
et tend vers 0, converge et on a, pour tout
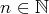 :
:
a)
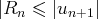 ;
;
b) la somme
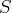 de la série est encadrée par deux sommes partielles consécutives
quelconques
de la série est encadrée par deux sommes partielles consécutives
quelconques
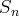 et
et
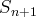 .
.
Exemple. Pour la série
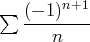 avec
avec
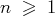 , on a
, on a
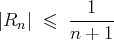 et
et
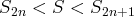 .
.
Soit
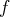 une fonction numérique définie et continue sur
une fonction numérique définie et continue sur
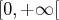 (ou à partir d’un
(ou à partir d’un
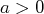 )
positive, décroissante et telle que
)
positive, décroissante et telle que
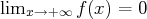 . La série de terme général
. La série de terme général
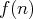 converge si et seulement si
converge si et seulement si
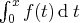 admet une limite quand
admet une limite quand
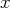 tend vers
tend vers
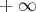 et l’on
a alors :
et l’on
a alors :
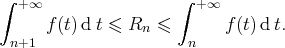
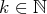 :
:
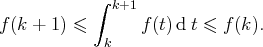
Exemple. Pour la série de terme général
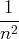 ,
,
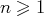 , avec la fonction
, avec la fonction
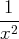 , on a :
, on a :
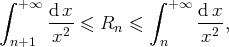
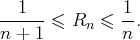
Soit
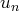 le terme général d’une série à termes positifs telle que la suite
le terme général d’une série à termes positifs telle que la suite
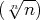 ait une limite
ait une limite
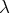 strictement inférieure à 1. La série est convergente et, en prenant un
strictement inférieure à 1. La série est convergente et, en prenant un
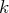 tel que
tel que
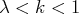 , il existe un entier
, il existe un entier
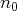 tel que, pour tout
tel que, pour tout
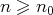 , on ait
, on ait
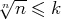 , donc
, donc
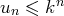 .
.
Pour tout
 , on peut donc majorer les termes du reste d’ordre
, on peut donc majorer les termes du reste d’ordre
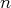 par les termes
d’une série géométrique de raison
par les termes
d’une série géométrique de raison
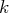 , c’est-à-dire :
, c’est-à-dire :
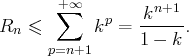
Exemple. Soit
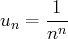 . Pour tout
. Pour tout
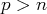 , on a
, on a
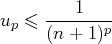 , d’où
, d’où
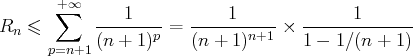
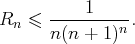
Soit
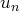 le terme général d’une série à termes strictement positifs telle que la suite
le terme général d’une série à termes strictement positifs telle que la suite
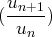 ait une limite
ait une limite
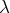 strictement inférieure à 1. La série est convergente et, en prenant un
strictement inférieure à 1. La série est convergente et, en prenant un
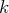 tel que
tel que
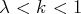 , il existe un entier
, il existe un entier
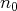 tel que, pour tout
tel que, pour tout
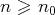 , on
ait
, on
ait
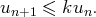
On en déduit que, pour tout
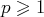 , on a
, on a
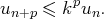
 , on peut donc majorer les termes du reste d’ordre
, on peut donc majorer les termes du reste d’ordre
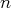 par les termes
d’une série géométrique de raison
par les termes
d’une série géométrique de raison
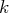 et :
et :