Primitives de
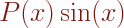
 s’écrit sous la forme
s’écrit sous la forme
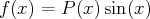 , où
, où
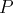 est une fonction
polynômiale, on calcule une primitive de
est une fonction
polynômiale, on calcule une primitive de
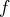 sur
sur
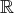 par une intégration par parties en
dérivant le polynôme.
par une intégration par parties en
dérivant le polynôme.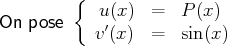
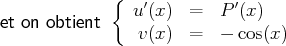
Les fonctions
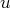 et
et
 ainsi définies sont bien continûment dérivables sur
ainsi définies sont bien continûment dérivables sur
 . On peut donc
appliquer la méthode d’intégration par parties et on a :
. On peut donc
appliquer la méthode d’intégration par parties et on a :
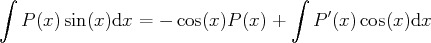
On se ramène donc au calcul d’une primitive d’une fonction qui est le produit
d’un polynôme de degré strictement plus petit que celui de
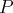 et de la fonction
cosinus.
et de la fonction
cosinus.
Si
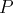 ’ est de degré zéro, alors on sait calculer une primitive de
’ est de degré zéro, alors on sait calculer une primitive de
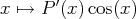 .
.
Sinon, on fait une nouvelle intégration par parties en dérivant
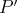 . On aboutit alors au calcul
d’une primitive de
. On aboutit alors au calcul
d’une primitive de
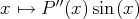 , c’est-à-dire qu’on a encore baissé le degré du
polynôme.
, c’est-à-dire qu’on a encore baissé le degré du
polynôme.
On recommence alors à faire des intégrations par parties en choisissant à chaque fois de
dériver le polynôme jusqu’à obtenir un polynôme constant.
Remarque. Tout ce qui précède s’applique aussi aux fonctions de la forme
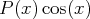 ,
,
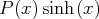 et
et
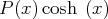 . Le calcul d’une primitive se fait en
utilisant des intégrations par parties où on dérive le polynôme.
. Le calcul d’une primitive se fait en
utilisant des intégrations par parties où on dérive le polynôme.
Exemple. Pour rechercher une primitive de la fonction
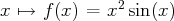 , on
fait une intégration par parties en posant
, on
fait une intégration par parties en posant
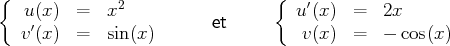
Les fonctions
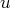 et
et
 ainsi définies sont bien continûment dérivables et on a :
ainsi définies sont bien continûment dérivables et on a :
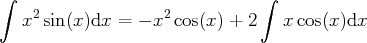
Pour calculer une primitive de
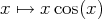 , on fait à nouveau une intégration par parties
en posant :
, on fait à nouveau une intégration par parties
en posant :
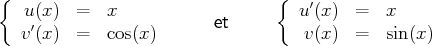
Les fonctions
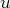 et
et
 ainsi définies sont bien continûment dérivables et on a :
ainsi définies sont bien continûment dérivables et on a :
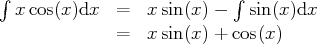
Finalement, on a trouvé qu’une primitive de
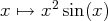 est
est
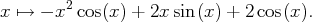
Remarque.
La méthode décrite ci-dessus montre aussi qu’une primitive de
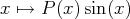 , où
, où
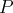 est
un polynôme de degré
est
un polynôme de degré
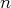 , peut s’écrire sous la forme
, peut s’écrire sous la forme
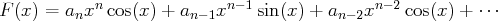
Dans le cas de cet exercice, on peut donc affirmer qu’une primitive de
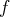 peut
s’écrire :
peut
s’écrire :
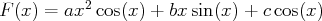
On utilise ensuite l’égalité
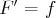 pour identifier les coefficients
pour identifier les coefficients
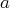 ,
,
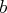 et
et
 .
.