Dessiner un escargot
 , où
, où
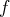 est une fonction continue, les points fixes de f
sont des candidats limites. Soit
est une fonction continue, les points fixes de f
sont des candidats limites. Soit
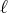 tel que
tel que
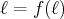 , un de ces candidats et supposons que,
dans un voisinage de
, un de ces candidats et supposons que,
dans un voisinage de
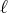 ,
,
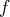 soit décroissante.
soit décroissante.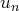 sont dans ce voisinage, ils prennent
successivement des valeurs supérieures et inférieures à
sont dans ce voisinage, ils prennent
successivement des valeurs supérieures et inférieures à
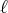 . Sur le graphique représentant
la fonction
. Sur le graphique représentant
la fonction
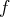 et la droite
et la droite
 les traits qui permettent de construire les éléments
successifs de la suite s’enroulent en forme d’escargot.
les traits qui permettent de construire les éléments
successifs de la suite s’enroulent en forme d’escargot.
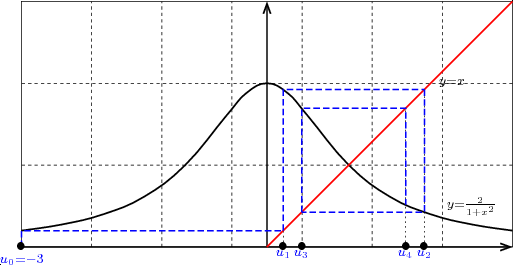
Dans cette situation il est naturel d’examiner séparément la suite des termes de rang
pair et la suite des termes de rang impair.
Il suffit de connaitre les positions relatives de
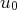 et
et
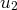 pour démontrer par récurrence,
en utilisant la décroissance de
pour démontrer par récurrence,
en utilisant la décroissance de
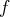 , la monotonie des suites des termes de rang
pair et impair. Par exemple : Si on sait que
, la monotonie des suites des termes de rang
pair et impair. Par exemple : Si on sait que
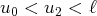 la décroissance de f
permet de montrer par récurrence la croissance de
la décroissance de f
permet de montrer par récurrence la croissance de
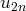 et la décroissance de
et la décroissance de
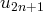 . Sur l’exemple du dessin on initialisera la récurrence par
. Sur l’exemple du dessin on initialisera la récurrence par
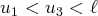 .
.
Pour obtenir la convergence de la suite
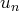 , il faut d’abord montrer que les suites
, il faut d’abord montrer que les suites
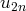 et
et
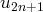 convergent vers la même limite. Une manière naturelle d’aboutir à ce résultat
est de passer à la limite dans les égalités :
convergent vers la même limite. Une manière naturelle d’aboutir à ce résultat
est de passer à la limite dans les égalités :
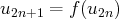 et
et
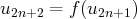 .
.
Pour montrer la convergence de
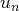 à partir de celle de
à partir de celle de
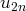 et
et
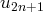 vers la même
limite, il est nécessaire de revenir à la définition de la convergence avec
vers la même
limite, il est nécessaire de revenir à la définition de la convergence avec
 .
.