Algèbre linéaire
Elément de cours des exercices
Les espaces de suites
 à valeurs dans
à valeurs dans
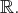 Elle est notée
Elle est notée
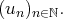


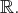 Il est de
dimension infinie.
Il est de
dimension infinie.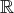 avec
les deux lois définies précedemment. Muni de l’addition et de la multiplication par un
complexe, c’est également un espace vectoriel sur
avec
les deux lois définies précedemment. Muni de l’addition et de la multiplication par un
complexe, c’est également un espace vectoriel sur
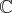 ; il est encore de dimension
infinie.
; il est encore de dimension
infinie.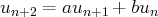 où
où
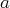 et
et
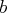 sont deux réels fixés, c’est un espace de
dimension 2 si
sont deux réels fixés, c’est un espace de
dimension 2 si
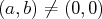 ;
;