Algèbre linéaire
Méthodes et techniques des exercices
Tester si une application linéaire est surjective
Définition : Une application d’un ensemble
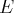 vers un ensemble
vers un ensemble
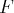 est dite
surjective si tout élément de
est dite
surjective si tout élément de
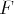 est l’image par
est l’image par
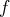 d’au moins un élément de
d’au moins un élément de
 .
.
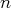 dans un espace de même
dimension. Dans un tel cas, dès qu’une application linéaire est injective, c’est à
dire dès que son noyau est réduit au vecteur nul, elle est bijective. Attention ! Ce
résultat est faux en dimension infinie.
dans un espace de même
dimension. Dans un tel cas, dès qu’une application linéaire est injective, c’est à
dire dès que son noyau est réduit au vecteur nul, elle est bijective. Attention ! Ce
résultat est faux en dimension infinie.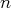 dans un espace vectoriel de dimension
dans un espace vectoriel de dimension
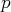 , avec
, avec
 est
surjective revient à tester que la dimension de son noyau est
est
surjective revient à tester que la dimension de son noyau est
 . Et si on
a
. Et si on
a
 , il n’existe pas d’application linéaire surjective de
, il n’existe pas d’application linéaire surjective de
 de dimension
de dimension
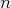 dans
dans
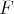 de dimension
de dimension
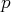 . (Théorème du rang).
. (Théorème du rang).
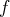 allant d’un espace
allant d’un espace
 dont on connaît
une base
dont on connaît
une base
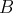 vers un espace
vers un espace
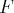 est surjective, il suffit de déterminer si l’image
par
est surjective, il suffit de déterminer si l’image
par
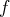 de
de
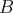 est une famille génératrice de
est une famille génératrice de
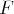 .
.
 quelconque dans l’ensemble d’arrivée,
peut-on trouver un
quelconque dans l’ensemble d’arrivée,
peut-on trouver un
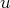 de l’ensemble de départ tel que
de l’ensemble de départ tel que
 s’écrive
s’écrive
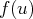 ? En général
on s’est fait une idée a priori.
? En général
on s’est fait une idée a priori.
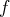 n’est pas surjective, on cherche un contre-exemple,
c’est à dire un
n’est pas surjective, on cherche un contre-exemple,
c’est à dire un
 qui ne pourra jamais s’écrire
qui ne pourra jamais s’écrire
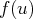 .
.
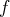 est surjective, on cherche un
est surjective, on cherche un
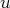 qui va nous
permettre d’arriver sur
qui va nous
permettre d’arriver sur
 .
.  de
de
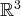 dans
dans
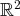 qui à
qui à
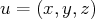 associe
associe
 est surjective, on choisit un vecteur
est surjective, on choisit un vecteur
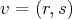 arbitraire. Et on observe que
arbitraire. Et on observe que
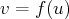 , avec
, avec
 ,
par exemple.
,
par exemple.