Équations différentielles
Méthodes et techniques des exercices
Exploitation de formulations intégrales dans l’étude d’équa diff
Pour les équations linéaires du premier ordre

 et
et
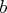 continues sur un intervalle ouvert
continues sur un intervalle ouvert
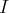 , la méthode de variation de la
constante permet, en désignant par
, la méthode de variation de la
constante permet, en désignant par
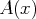 une primitive de
une primitive de
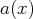 sur
sur
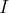 , d’écrire les
solutions sur
, d’écrire les
solutions sur
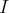 :
:
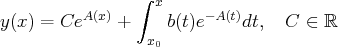
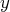 à partir de cette expression (majoration, limites,
à partir de cette expression (majoration, limites,
 ).
).
Pour les équations linéaires du second ordre à coefficients constants
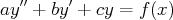
 à l’aide d’intégrales qui permettent parfois d’obtenir des propriétés de
à l’aide d’intégrales qui permettent parfois d’obtenir des propriétés de
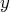 sans calculer ces intégrales.
sans calculer ces intégrales.
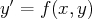
Pour les équations du premier ordre

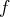 est une fonction continue, on remplace la recherche de solutions vérifiant la
condition de Cauchy
est une fonction continue, on remplace la recherche de solutions vérifiant la
condition de Cauchy
 par la recherche de solutions de l’équation intégrale
équivalente
par la recherche de solutions de l’équation intégrale
équivalente
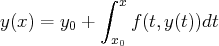
Elle permet aussi, éventuellement en utilisant le Lemme de Gronwall, d’obtenir des propriétés
de la solution
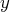 quand on ne sait pas la calculer explicitement.
quand on ne sait pas la calculer explicitement.

Dans certains cas, une équation différentielle
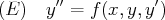
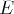 quand on ne sait pas les calculer
explicitement.
quand on ne sait pas les calculer
explicitement.
Exemple. Soit l’équation différentielle
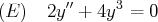
On multiplie par
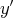 et on intègre sur
et on intègre sur
![[x0,x ]](cst29x.png) où
où
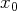 est un réel fixé dans l’intervalle
de définition de la solution considérée
est un réel fixé dans l’intervalle
de définition de la solution considérée
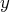 ; on obtient
; on obtient

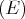 est bornée.
est bornée.
Attention : Ici nous obtenons une formulation intégrale qui n’est pas équivalente à l’équation différentielle de départ.