Arithmétique des entiers

Éléments de solutions et résultats de l'exercice numéro 3.2

On construit un tableau des entiers entre 200 et 249 et on surligne en rouge tous les nombres pairs :

De même maintenant tous les nombres divisibles par 3, et tous les nombres divisibles par 5 :

Sachant que 210 est divisible par 7, on surligne en rouge alors les autres multiples de 7 : 210-7, puis 210+7. . ..

On surligne ensuite les multiples de 11 : 220 est divisible par 11 ; on surligne alors 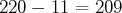. Les autres multiples de 11 ont déjà été surlignés.
On surligne également les multiples de 13 : 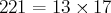. C'est le seul multiple de 13 qui ne soit pas encore surligné dans le tableau.

Le nombre premier suivant 13 est 17, or 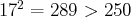. Donc les nombres non rouges du tableau sont des nombres premiers.
Il ne reste alors plus que deux couples possibles de nombres jumeaux : (227,229) et (239,241).
Ce sont les seuls compris entre 200 et 250.